Definition of fuzzy logic: Fuzzy logic, a powerful tool in computational intelligence, differs significantly from traditional binary logic. Instead of strict true/false values, fuzzy logic uses membership degrees ranging from 0 to 1, representing the degree of truth or certainty. This allows for more nuanced reasoning, making it exceptionally useful in situations involving uncertainty and imprecision. This exploration delves into the core concepts, historical context, and applications of fuzzy logic, highlighting its advantages and limitations.
Fuzzy logic’s ability to handle vague and imprecise information sets it apart. It allows for the development of systems that can reason and make decisions based on a spectrum of possibilities, rather than just absolute certainties. Imagine controlling a washing machine not just with ‘on’ or ‘off’ but with adjustable settings based on factors like water temperature. This sophisticated approach is at the heart of fuzzy logic.
Introduction to Fuzzy Logic
Fuzzy logic is a powerful approach to decision-making that differs significantly from traditional binary logic. Instead of relying on strict true/false classifications, fuzzy logic allows for degrees of truth, enabling more nuanced and flexible reasoning. This flexibility makes it particularly well-suited for applications where human-like reasoning is desirable, such as control systems and expert systems. It’s a framework for dealing with uncertainty and vagueness, a common characteristic of real-world problems.This flexibility stems from the ability to represent concepts with varying degrees of membership.
Consider the concept of “warm”. In binary logic, something is either “warm” or “not warm”. In fuzzy logic, we can assign varying degrees of membership to the concept “warm” based on temperature. A temperature of 20°C might have a low membership to “warm,” while 30°C might have a high membership. This gradation allows for more realistic and adaptable responses.
Definition of Fuzzy Logic
Fuzzy logic extends the concept of “true” and “false” to encompass a spectrum of possibilities. A core concept is the membership function, which quantifies the degree to which an element belongs to a set. This function assigns a value between 0 and 1 to each element, with 0 indicating no membership and 1 indicating full membership. This continuous spectrum allows for gradual transitions and imprecise classifications.
Fuzzy sets are collections of elements with varying degrees of membership, rather than crisp, definitive sets.
Difference between Fuzzy Logic and Binary Logic
Binary logic, the foundation of digital computing, operates on a simple principle: a statement is either true or false. This “all-or-nothing” approach is suitable for digital circuits where clear distinctions are crucial. Fuzzy logic, on the other hand, allows for degrees of truth, enabling more nuanced and flexible reasoning.
| Feature | Binary Logic | Fuzzy Logic |
|---|---|---|
| Values | True/False | Membership degrees (0-1) |
| Reasoning | Crisp rules | Fuzzy rules |
| Applications | Digital circuits | Control systems, expert systems |
Historical Context and Evolution
Fuzzy logic emerged from the work of Lotfi Zadeh in the 1960s. Zadeh’s introduction of fuzzy sets provided a mathematical framework for handling vagueness and uncertainty. Initially, fuzzy logic was met with skepticism, but its potential was quickly recognized. Its practical applications in areas like control systems and expert systems have significantly advanced its adoption over the years.
Fuzzy Sets and Membership Functions

Fuzzy logic, unlike traditional logic, deals with degrees of truth rather than absolute truth or falsehood. This is elegantly handled through the concept of fuzzy sets and membership functions. These tools allow us to model imprecise or vague concepts in a quantitative way, making them applicable in diverse fields.
Understanding Fuzzy Sets
Fuzzy sets extend the concept of crisp sets. In a crisp set, an element either completely belongs or does not belong to the set. Fuzzy sets, however, allow for partial membership. An element can have a degree of membership in a fuzzy set, ranging from 0 (no membership) to 1 (complete membership). This degree is quantified by a membership function.
For example, consider the fuzzy set “tall people.” A person of 6 feet might have a high degree of membership, while a person of 5 feet might have a low degree of membership.
Membership Functions: Defining Degrees of Membership
Membership functions are mathematical functions that map elements from the universe of discourse to a membership value between 0 and 1. They essentially define the degree to which an element belongs to a fuzzy set. Different types of membership functions offer various shapes and characteristics, each suitable for different scenarios.
Common Types of Membership Functions
Several types of membership functions are frequently used in fuzzy logic applications. Their shapes reflect different ways of modeling the degree of membership.
- Triangular Membership Function: This function is characterized by three parameters: a, b, and c. These parameters define the vertices of a triangle, with the membership value increasing from 0 to 1 as the input value moves from a to c. The function is defined as 0 for values outside the triangle. For example, consider the fuzzy set “temperature.” A triangular function could model the degree of membership for “cold,” “moderate,” or “hot” temperatures.
A triangular function is useful when there is a clear, well-defined range of values that gradually transition to one another.
- Trapezoidal Membership Function: Similar to the triangular function, the trapezoidal function is defined by four parameters: a, b, c, and d. These parameters define the vertices of a trapezoid. The membership value is 1 within the interval [b, c] and smoothly transitions to 0 outside the interval [a, d]. This function is beneficial for modeling imprecise ranges, where a certain interval has complete membership, and the values outside the interval smoothly transition to 0 membership.
A trapezoidal function can be used to model fuzzy sets like “average speed” where there is a well-defined range of acceptable speeds.
- Gaussian Membership Function: The Gaussian function is a bell-shaped curve. It’s defined by two parameters: the mean (μ) and the standard deviation (σ). The mean represents the center of the curve, and the standard deviation controls the spread. A Gaussian function is excellent for modeling fuzzy sets where the membership value drops off gradually as the input deviates from the mean.
Consider a fuzzy set representing “customer satisfaction.” A Gaussian function could model the satisfaction level around a particular mean score, with lower satisfaction levels having progressively smaller membership values.
Examples and Applications
Consider the fuzzy set “age.” A triangular membership function might be used to model the fuzzy set “young,” where the range of young ages is well-defined. Similarly, a trapezoidal function could model the fuzzy set “middle-aged,” defining the range of ages with complete membership. A Gaussian function could model the fuzzy set “senior citizen,” capturing the gradual decrease in membership as age deviates from the mean.
Illustrative Table of Membership Functions
| Function Type | Mathematical Form | Graph |
|---|---|---|
| Triangular |
|
A triangle with vertices at (a, 0), (b, 1), and (c, 0). |
| Trapezoidal |
|
A trapezoid with vertices at (a, 0), (b, 1), (c, 1), and (d, 0). |
| Gaussian |
|
A bell-shaped curve centered at μ, with the spread controlled by σ. |
Fuzzy Rules and Inference Systems
Fuzzy logic takes a different approach to decision-making compared to traditional, crisp logic. Instead of strict, binary classifications (true or false), fuzzy logic allows for degrees of truth. This flexibility is particularly useful in real-world applications where precise measurements or conditions are difficult to define. Fuzzy rules form the core of fuzzy inference systems, enabling these systems to handle uncertainty and imprecision in a sophisticated way.Fuzzy rules are essentially “if-then” statements that map input values to output values.
They incorporate linguistic variables and fuzzy sets, enabling the representation of vague concepts like “warm,” “medium,” or “high.” These rules are used in many applications, including temperature control, medical diagnosis, and financial modeling. Their adaptability makes them invaluable for situations where precise mathematical models are not readily available or suitable.
Structure of Fuzzy Rules
Fuzzy rules typically follow an “if-then” structure, linking input conditions (antecedents) to output actions (consequents). The antecedents and consequents are often expressed using fuzzy sets, allowing for degrees of membership. For instance, a rule might state: “If the temperature is warm, then set the thermostat to medium.” This rule uses a fuzzy set for “warm” to describe a range of temperatures, rather than a precise value.
Examples of Fuzzy Rules
Consider a simple temperature control system for a greenhouse. The following fuzzy rules demonstrate how linguistic variables can be used to control the environment:
- If the temperature is cold, then increase the heater output.
- If the temperature is warm, then maintain the current heater output.
- If the temperature is hot, then decrease the heater output.
These rules, using fuzzy sets for “cold,” “warm,” and “hot,” provide a more flexible and robust control system than a system based on fixed temperature thresholds.
Steps in Fuzzy Inference Systems
Fuzzy inference systems use a specific set of steps to map inputs to outputs:
- Fuzzification: The input values are mapped to membership functions of fuzzy sets. For example, a temperature sensor reading of 22°C might be classified as “warm” with a degree of membership of 0.8, and “cool” with a degree of membership of 0.2.
- Rule Evaluation: The fuzzy inference system evaluates each fuzzy rule. The degree of truth for each rule is determined by the degree of membership of the input values in the corresponding fuzzy sets. For example, if the temperature is “warm” (0.8 membership), the rule “If the temperature is warm, then set the thermostat to medium” will have a truth value of 0.8.
- Inference: The system combines the results of the rule evaluations. This often involves using fuzzy operators, such as “and” and “or,” to combine the truth values of multiple rules.
- Defuzzification: The output of the inference process is a fuzzy set. To obtain a crisp output value, a defuzzification method is applied. Common methods include centroid, mean of maximum, or weighted average. For example, if the defuzzification process determines that the output value is “medium,” the system can then translate this fuzzy value into a specific thermostat setting.
These steps are crucial in allowing the system to handle the ambiguity of fuzzy sets.
Mapping Inputs to Outputs Using Fuzzy Rules
Fuzzy rules act as a bridge between the input and output. The inputs are mapped to fuzzy sets, and the rules determine the degree to which each consequent is activated. The overall output is a fuzzy set that represents the combined effect of all the rules. Defuzzification converts this fuzzy output into a precise numerical value. This process effectively transforms vague input conditions into precise control actions.
Washing Machine Control Example
IF water temperature is COLD THEN set water heater to HIGH.IF water temperature is WARM THEN set water heater to MEDIUM.IF water temperature is HOT THEN set water heater to LOW.
This example demonstrates a simple fuzzy rule set for a washing machine. The input “water temperature” is categorized into fuzzy sets like “COLD,” “WARM,” and “HOT.” The output, the water heater setting, is also categorized into fuzzy sets (“HIGH,” “MEDIUM,” and “LOW”). The rules translate the input temperature to an appropriate heater setting.
Applications of Fuzzy Logic: Definition Of Fuzzy Logic
Fuzzy logic, with its ability to handle uncertainty and vagueness, has found widespread application across diverse fields. Its capacity to model human reasoning and decision-making processes makes it a powerful tool in situations where precise mathematical models are inadequate or impractical. This adaptability allows for more robust and flexible solutions compared to traditional approaches.
Fuzzy logic, in a nutshell, deals with degrees of truth rather than absolute yes or no answers. It’s fascinating how this concept, seemingly abstract, can be applied to real-world scenarios, like the complex dynamics explored in the insightful documentary one to one John and Yoko documentary. Ultimately, fuzzy logic provides a powerful tool for handling uncertainty and ambiguity in a way that’s increasingly important in modern technology.
Fuzzy Logic in Control Systems
Fuzzy logic control systems excel in scenarios where precise mathematical models are unavailable or excessively complex. They offer an alternative to conventional control methods by leveraging linguistic variables and fuzzy rules. This approach mimics human decision-making, allowing the system to adapt to changing conditions and uncertainties. For instance, a fuzzy logic controller can regulate the temperature of a furnace more effectively than a traditional controller if the relationship between the input (fuel flow) and the output (temperature) is not precisely known.
Fuzzy Logic in Decision-Making
Fuzzy logic’s ability to model human reasoning is invaluable in complex decision-making processes. In uncertain environments, where precise data is limited or unavailable, fuzzy logic excels by providing a framework for incorporating expert knowledge and subjective judgments. A fuzzy system can be trained with examples of expert decisions to learn the underlying reasoning patterns, leading to more informed and robust decisions.
For example, in medical diagnosis, a fuzzy system can integrate various symptoms and patient history, even if the relationship between these factors is not fully understood, to provide a more comprehensive assessment compared to a system relying solely on precise data.
Fuzzy Logic in Robotics
Fuzzy logic’s adaptability is particularly advantageous in robotics applications. Traditional control systems often struggle with complex and dynamic environments. Fuzzy logic provides a flexible framework for robot navigation, allowing for the consideration of various factors, such as obstacles, terrain, and desired trajectory. The system can adapt to unexpected changes in the environment, enabling robots to perform tasks more effectively and safely.
For instance, a robot navigating a cluttered room can use fuzzy logic to adjust its path based on proximity to obstacles, ensuring a smooth and safe movement.
Fuzzy logic, essentially, deals with degrees of truth rather than strict binary values. It’s like trying to understand the nuanced responses of world leaders to the recent Trump tariffs reversal, and the subsequent uncertainty surrounding the trade war, as seen in this article. Ultimately, fuzzy logic provides a framework for handling imprecise information, a valuable tool for navigating complex situations like international trade disputes.
Fuzzy Logic in Consumer Electronics
Fuzzy logic has significantly improved the functionality of various consumer electronic devices. Washing machines, for example, use fuzzy logic to adjust water temperature, spin speed, and wash time based on the type of fabric and level of dirt. This leads to more efficient and effective cleaning, saving energy and resources. Other appliances, like dishwashers, air conditioners, and refrigerators, can also leverage fuzzy logic to optimize their operations and improve user experience.
Fuzzy Logic vs. Traditional Control Systems
Traditional control systems rely on precise mathematical models and calculations. Fuzzy logic, on the other hand, utilizes linguistic variables and fuzzy rules, enabling it to handle uncertainty and vagueness more effectively. While traditional systems often require extensive mathematical modeling, fuzzy systems can be developed using expert knowledge and examples, making them simpler and more intuitive to design in some cases.
The choice between the two depends heavily on the specific application and the available information.
Applications Table
| Industry | Application | Description |
|---|---|---|
| Consumer Electronics | Washing machine control | Fuzzy logic adjusts water temperature, spin speed, and wash time based on fabric type and dirt level, optimizing the wash cycle and saving energy. |
| Robotics | Navigation | Fuzzy logic allows robots to navigate complex environments by adjusting their path based on obstacles, terrain, and desired trajectory, ensuring smoother and safer movement. |
| Finance | Risk assessment | Fuzzy logic can assess risk by considering various factors, such as market trends, economic indicators, and expert opinions, providing a more comprehensive and nuanced evaluation compared to purely quantitative models. |
| Automotive | Automatic Transmission Control | Fuzzy logic can optimize gear shifting based on vehicle speed, acceleration, and driver behavior, leading to a smoother and more efficient driving experience. |
Advantages and Disadvantages of Fuzzy Logic
Fuzzy logic, a powerful tool for handling imprecise and vague information, has found applications across diverse fields. It offers a unique approach to decision-making, particularly in situations where traditional, crisp logic struggles. However, like any methodology, fuzzy logic has its limitations. This section explores the strengths and weaknesses of fuzzy logic, comparing it to traditional methods and highlighting the challenges and opportunities associated with its implementation.
Advantages of Fuzzy Logic
Fuzzy logic excels in situations where the relationships between input and output are not easily defined by precise mathematical equations. Its ability to handle linguistic variables and approximate reasoning makes it suitable for tasks that are difficult to model using traditional methods. This flexibility is crucial in many real-world applications. For instance, controlling a complex system like a robot arm, where precise mathematical models might be unavailable, is greatly aided by fuzzy logic.
The approach allows for intuitive rule-based systems, making the system easier to understand and modify.
Fuzzy logic, essentially, deals with degrees of truth rather than absolute ones. It’s fascinating to consider how this concept might apply to the current climate debate, particularly when examining President Trump’s policies. For example, the article has trump accidentally ushered in an era of climate pragmatism highlights how seemingly contradictory actions can lead to unintended outcomes.
Ultimately, understanding fuzzy logic’s implications requires a nuanced perspective, similar to analyzing complex political situations.
- Improved Decision-Making in Complex Systems: Fuzzy logic excels in situations where the relationships between variables are not clearly defined by precise mathematical equations. It handles uncertainty and ambiguity effectively, leading to better decision-making in complex systems. This is particularly useful in areas like control systems and expert systems where traditional methods struggle to capture the nuanced nature of the problem.
- Simplified System Design and Implementation: Fuzzy logic often results in simpler and more understandable control systems compared to traditional methods. The use of linguistic variables and rules makes the system easier to design, implement, and maintain. This can significantly reduce development time and costs, especially in applications with limited expertise in the underlying system.
- Robustness and Adaptability: Fuzzy systems are generally more robust than traditional systems. They can handle noisy data and uncertainties better, adapting to changing conditions without requiring extensive reprogramming. This adaptability is critical in real-world applications where the environment is not static.
Disadvantages of Fuzzy Logic
Despite its advantages, fuzzy logic faces certain limitations. One key concern is the subjectivity inherent in defining membership functions. The quality of the output depends heavily on the expertise and judgment used in defining these functions, which can introduce inconsistencies and make the system less reliable. Also, the lack of a clear mathematical framework can make it difficult to analyze the system’s behavior in a quantitative way.
Furthermore, fuzzy logic systems can be computationally intensive, especially for complex applications.
- Subjectivity in Membership Function Definition: Defining membership functions for fuzzy sets requires expertise and judgment. Different experts might create different membership functions, leading to inconsistencies in the system’s output. This subjectivity can be a significant drawback, impacting the reliability and consistency of the system.
- Lack of a Clear Mathematical Framework: Fuzzy logic lacks a precise mathematical framework. This can make it challenging to analyze the system’s behavior quantitatively and rigorously. This lack of a strong mathematical foundation can limit the application’s ability to handle complex and dynamic situations.
- Computational Complexity: Fuzzy logic systems can be computationally intensive, particularly for complex applications. This computational overhead can be a significant limitation in real-time applications where quick response times are critical.
Comparison with Traditional Methods
Traditional methods, such as classical control theory, often rely on precise mathematical models. These models can be accurate in well-defined environments but struggle in complex, uncertain situations. Fuzzy logic, on the other hand, offers a more intuitive and adaptable approach. For instance, in a self-driving car, fuzzy logic can be used to control the steering and braking based on sensor inputs like speed, distance, and obstacles, even in unpredictable traffic conditions, whereas a purely mathematical model might struggle to accommodate such a high degree of unpredictability.
The choice between fuzzy and traditional methods often depends on the specific application and the trade-offs between accuracy, complexity, and adaptability.
Challenges and Opportunities
Implementing fuzzy logic systems requires careful consideration of the application domain. A key challenge lies in the design and tuning of the fuzzy rules. Finding the optimal set of rules that accurately capture the desired behavior requires experimentation and expertise. However, the opportunities are significant. Fuzzy logic can potentially improve decision-making in many fields, including robotics, medicine, and finance, leading to more robust and adaptable systems.
In addition, advancements in computing power and AI could further enhance the capabilities of fuzzy logic systems.
Summary Table
| Feature | Advantages | Disadvantages |
|---|---|---|
| Implementation | Relatively easier to implement in some cases, intuitive rules. | Complex systems can be challenging to implement and require significant expertise. |
| Accuracy | Suitable for imprecisely defined systems, can provide high accuracy in appropriate situations. | Accuracy can vary depending on the expertise in defining membership functions, can be less precise than traditional methods in well-defined scenarios. |
Fuzzy Logic and Computational Intelligence
Fuzzy logic, a powerful tool in computational intelligence, excels at handling imprecise and vague information. Its ability to model human reasoning makes it well-suited for a variety of applications, especially where traditional, crisp logic falls short. This section explores the connections between fuzzy logic and other computational intelligence techniques, highlighting how fuzzy logic can be combined with other AI methods to tackle complex problems.
Relationship with Other Computational Intelligence Techniques
Fuzzy logic shares a close relationship with other computational intelligence methods, often working synergistically. Its ability to handle uncertainty complements the strengths of neural networks and evolutionary algorithms. For instance, fuzzy logic can provide a more intuitive and understandable framework for interpreting the outputs of neural networks, making them more accessible and usable in real-world applications.
Combining Fuzzy Logic with Other AI Methods
Fuzzy logic can be seamlessly integrated with other AI methods to enhance their capabilities. One common approach is to use fuzzy logic to define the input and output parameters of a neural network. This allows the neural network to learn complex relationships between variables while ensuring the input and output values are appropriately interpreted. Another approach involves using fuzzy rules to guide the search process in evolutionary algorithms, leading to more efficient and effective solutions.
This combination allows for more complex and nuanced problem-solving.
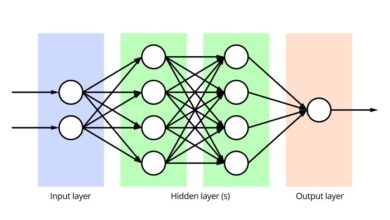
Fuzzy Logic and Neural Networks: A Comparison
Fuzzy logic and neural networks, while both powerful AI techniques, have distinct characteristics. Fuzzy logic excels at modeling human reasoning, providing transparency and interpretability to the decision-making process. Neural networks, on the other hand, are capable of learning complex patterns and relationships in data, but their internal workings are often opaque. Fuzzy logic’s strength lies in its ability to explicitly define the relationships between variables, while neural networks excel at capturing complex, non-linear relationships in large datasets.
Illustration: Fuzzy Logic in a Traffic Control System
Consider a traffic control system for a busy intersection. Traditional control systems often rely on fixed rules based on traffic volume. However, real-world traffic patterns are complex and unpredictable, influenced by various factors like weather, time of day, and special events. Fuzzy logic can be integrated with a neural network to create a more adaptable and intelligent traffic control system.
- The neural network analyzes real-time traffic data, including vehicle density, speed, and direction.
- Fuzzy logic rules, based on traffic volume, road conditions, and weather, define the appropriate actions for traffic signals.
- The system adjusts traffic signal timing dynamically, optimizing flow and minimizing congestion.
- For example, during heavy rain, the neural network might detect decreased visibility and increased accident risk. Fuzzy logic rules would then adjust signal timings to increase safety and reduce congestion.
This integrated approach combines the learning capabilities of a neural network with the interpretability and human-like reasoning of fuzzy logic, leading to a more sophisticated and effective traffic control system compared to traditional methods.
Conclusive Thoughts
In summary, fuzzy logic offers a flexible and powerful alternative to traditional binary logic, particularly well-suited for complex systems involving uncertainty. Its application spans numerous fields, from consumer electronics to robotics and finance, demonstrating its versatility and effectiveness. While it has its limitations, fuzzy logic continues to evolve and find new applications in an increasingly complex world.